【ゼロから始めるデータ分析#2】データ分析初心者が覚えておくべき3つの分析手法

これまでデータ分析を学んだことがない方に向けて、データ分析の基礎知識を解説していく本連載。
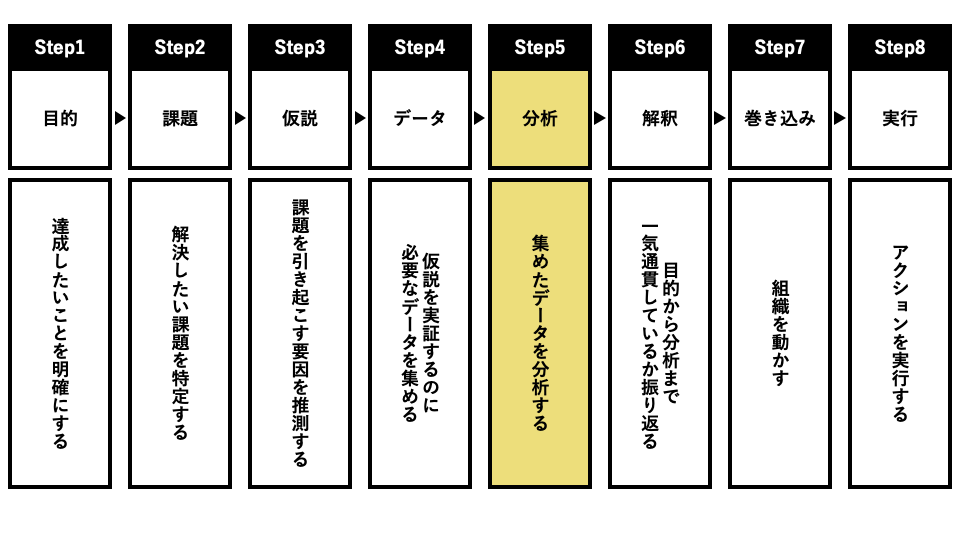
第1回では、データ分析の基本となる8ステップを解説しました。
【ゼロから始めるデータ分析#1】データ分析初心者初学者がまず知るべき「分析の8ステップ」

第2回となる今回は、このうちの「Step5:分析」に焦点をあて、データ分析初心者が覚えておきたい3つの分析手法を紹介します。
↓ 「ゼロから始めるデータ分析」記事一覧はこちら ↓
#1 初学者がまず知るべき「分析の8ステップ」
#2 データ分析初心者が覚えておくべき3つの分析手法
#3 データ分析初心者が知っておきたい、経営層を巻き込むコミュニケーションのポイント
#4 データ分析初心者が知っておきたい、経営層がデータ分析と分析担当者に求めるもの
#5 データ分析初心者でも経営と組織を巻き込める、現場担当者のための4つのTips
目次
ビジネスで使える、3つの分析手法
ビジネスパーソンがなぜデータ分析をするのか? と聞くと、
「売上につながる要因を特定したい」「投資効果を数値で確認したい」
といった思いが背景にあることがほとんどだと思います。
これらはいずれも、売上とそれぞれの要因、 投資額とその効果というように「データとデータの結びつきの強さを数値化・可視化したい」という要望であると言い換えられます。
データ分析(統計分析)は、このようにデータとデータの結びつきの強さから影響度合いを数値化・可視化することを得意とします。
データ分析の手法は数多くありますが、今回は、データ分析初心者が覚えておいて損はない、比較的簡単な「クロス集計」「単回帰分析」「重回帰分析」の3つの分析手法について紹介していきます。
データ分析の基本「クロス集計」
仮説に合わせて、さまざまな切り口でデータを掛け合わせ、分析する手法が「クロス集計」です。
クロス集計は、特別な統計知識も、難しい数式も、特殊な解析ソフトも必要なく、初心者の方でも明日から取り組んでいただける分析手法です。しかし、その分かりやすさとは裏腹に、データ分析の領域で「クロス集計を制する者がデータ分析を制す」という言葉があるほど重要な、データ分析の基本となる分析手法です。
(e.g.)アイスメーカーが女性向けキャンペーンの実施を決定。キャンペーンの対象商品を決めるためにデータ分析を試みた
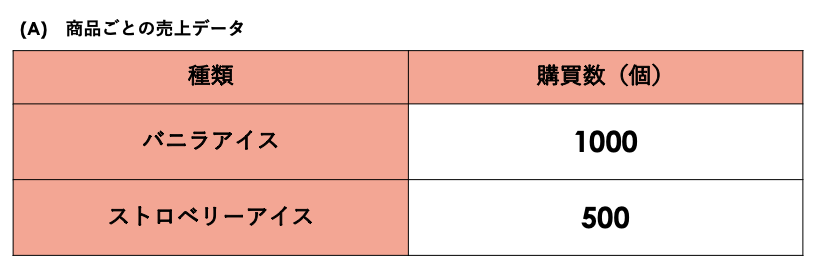
キャンペーンの対象商品として候補に挙がっているバニラアイスとストロベリーアイスの売上データを比較してみると、バニラアイスがストロベリーアイスの2倍の売上を占めています。このデータだけを見たら、バニラアイスをキャンペーンの対象商品にしようと思うかもしれません。
ですが、今回はターゲットを女性にしぼったキャンペーンです。そこで、性別ごとの売上データを見てみると、女性よりも男性のほうが購買数が多いことが分かります。

そこで、購入者の性別ごとに売上データを見てみましょう。すると、バニラアイスの購入者の9割は男性で、一方のストロベリーアイスは、購入者の8割が女性でした。この結果を受け、 今回の女性向けキャンペーンの対象商品はストロベリーアイスに決定しました。
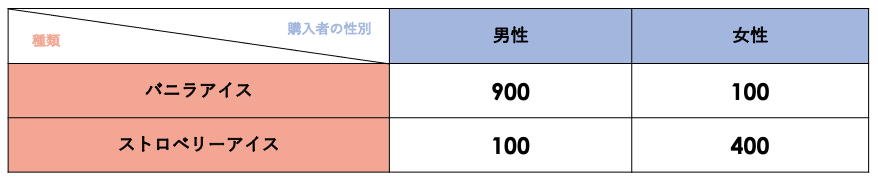
クロス集計はこのように、データをタグ(性別・年齢・嗜好など)で分類し、それらを掛け合わせて行う分析です。
1対1の関係性の強さを導き出す「単回帰分析」
“身長”と“体重”、 “最寄り駅からの距離”と“賃貸住宅の家賃”のように、仮説の時点で関係性が強いと予想される2つのデータの関係性の強さを導き出す分析手法が「単回帰分析」です。
一般的には、単回帰分析を行う前に、データとデータの相関の強さを表す「相関係数」を算出し、相関関係の有無を確認するところから始めます。相関係数はエクセルの標準数式を使って算出することができ、−1(完全な負の相関)から+1(完全な正の相関)の間の数値になります。

相関関係の有無は、相関係数の数値によって以下のように判断します。
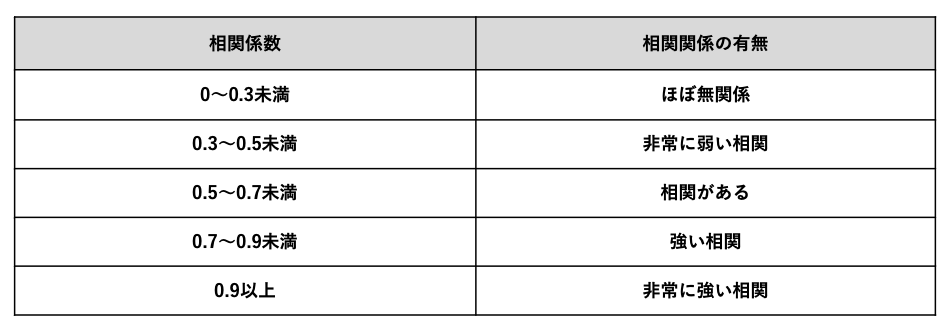
2つのデータの相関関係は、比例もしくは反比例の関係にあるので、分析のアウトプットとしては、「一方が大きくなるともう一方も大きくなる」「一方が大きくなると他方が小さくなる」「相関なし」のいずれかになります。
「相関」というのは単なる関係性の有無なので、2つのデータの間に原因→結果があるかないかは関係ありません。一方の「単回帰分析」は、片方のデータが1増えるともう片方のデータがどのくらい増えるかといった、2つのデータの原因と結果の関係を求めるものです。
2つのデータの相関の規則性を視覚的に確認するためには、「散布図」というグラフを使います。データが該当するところにプロット(打点)していき、これらの点の傾向を表す傾向線を引くと、線の傾きの大きさで、2つのデータの関係(xが1増えると、yはどのくらい増えるか)を可視化できます。

また、2つのデータの関係を数値化したものを「回帰係数」といいます。
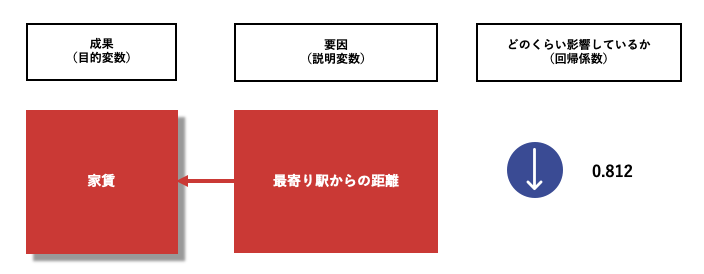
Point)単回帰分析は、売上予測には向かない
ビジネスの現場で、1つの要因と1つの成果のみが存在する状況はほとんどありません。たとえば、テレビCMがどのくらい売上に影響を与えたかを知りたいときに、テレビCMの出稿量と売上高のデータを使って単回帰分析をしても、精度の高い予測は見込めません。実際は、新聞広告やインターネット広告など、ほかの広告施策、立地や天候、値下げセールなど、さまざまな条件が売上に影響を与えているからです。売上予測には、次項で紹介する重回帰分析を使うことをおすすめします。
複数の要素の関係性を見出す「重回帰分析」
「重回帰分析」は「単回帰分析」と同じく、成果と要因の関係性を導き出す「回帰分析」の仲間です。単回帰分析が2つのデータの相関関係を探るのに対し、重回帰分析は3つ以上データの相関関係を導き出します。
ビジネスの現場では、
「売上目標を達成するためには、広告宣伝費にいくらかけるべきか」
「施策Aと施策B、それぞれどのくらいの効果が見込めるか」
「今期の予算をどう配分すると、マーケティング成果を最大化できるか」
というように、複数の要因を統合的に分析した上でアクションを検討すべき場面が多くあります。
重回帰分析は、こういった売上予測やマーケティング戦略の策定などに活用できる、マーケティング分野では必須ともいえる分析手法。 成果に影響を与えていると予想される3つ以上の要因(=説明変数)を、成果(=目的変数)に掛け合わせ、それぞれの相関関係のあり・なし、関係性の強さ・弱さを導き出す分析です。
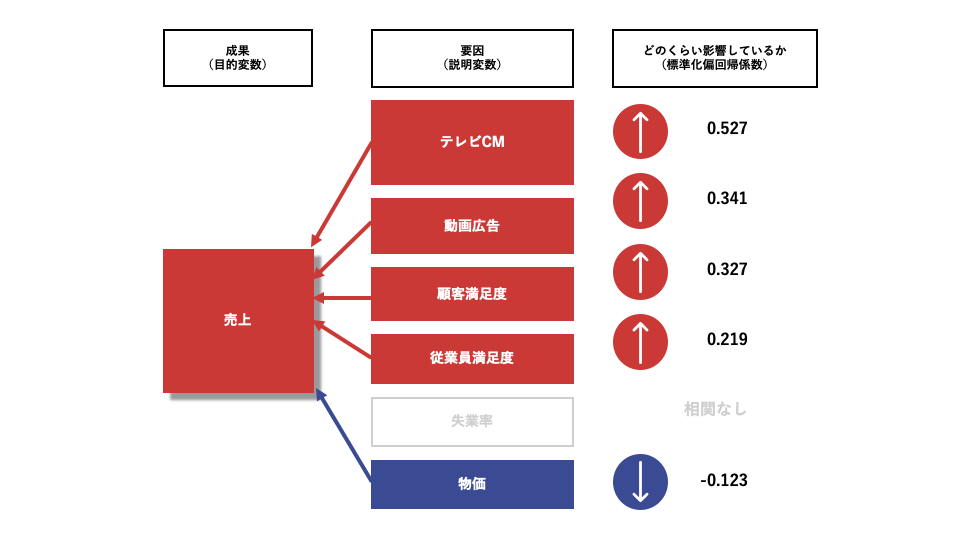
※ 標準化と標準化偏回帰係数:成果に影響を与えている要因(説明変数)は、それぞれ単位が違います。そこで、それぞれの変数を特定の値になるように調整します。このことを「標準化」といい、標準化によって求められる「標準化偏回帰係数」は、平均を0、分散を1で表し、数値間の大小で相対的に各変数の影響度合いを評価します。
(e.g.)マーケティング施策の最適な予算配分を検討するため、重回帰分析を行う
① 今回の分析で知りたいこと(何らかの施策を通じて増やしたい、もしくは減らしたいこと)を成果(目的変数)として設定します
例)最適な予算配分でマーケティング施策を実行し売上を上げたい場合は、「売上」を目的変数におきます
② 最終的な成果(目的変数)に影響を与えていそうな複数の要因(説明変数)を洗い出します(説明変数は10以内におさめます)
③ それぞれのデータを収集し、統計ソフトで分析します
※ エクセルのデータタブにある「回帰分析」ツールや、「JMP」や「SPSS」などの有料ソフトを使います
④ 算出された方程式(重回帰式といいます)に、計画している施策の予算を入れ、各施策の最適な予算を探ります
Point)重回帰分析は、説明変数同士で相関関係が強いものを入れてしまうとうまくいかない(多重共線性)
重回帰分析を行う際、分析精度を上げようと、たくさんの説明変数を入れてしまうことがあります。ですが、説明変数同士で相関関係の強いものがあると「多重共線性」という現象が起き、予測精度が低下します。多重共線性は、英語で「multicollinearity」ということから、略して「マルチコ」とも呼ばれます。
(e.g.)「コンビニの月間売上(成果)」に関係がありそうな要因として「月間の降水量」と「雨が降った日数」を説明変数に入れて重回帰分析を行った
→「月間の降水量」と「雨が降った日数」の相関関係が非常に高いため(雨が降った日数が多ければ月間降水量も増える)、多重共線性が発生する
<多重共線性が発生してしまった場合の回避方法 >
①相関関係が強い要因のうち、どちらか一方を外して再度分析する(どちらを外すか迷った場合は、仮説に沿って優先度の高い方を残す。または両方を一つずつ入れて分析してみる)
②変数同士の性質が同じ場合(たとえば、動画Aと動画Bを変数として入れたい場合など)は、両者を統合(足し算)した数値を使って分析する
データ分析をゼロから学びたい人におすすめの書籍2選
『やさしく学ぶ データ分析に必要な統計の教科書』羽山 博(著)
エクセルを活用した分析のやり方など、実践的なHOWTOを学べます。はじめてデータ分析に触れる方が、データ分析の基礎を学びたいと思ったときにおすすめの一冊です。
『統計学図鑑』栗原 伸一 ・丸山 敦史 (著)
教科書に載っているようなデータ分析手法を、噛み砕いて説明してくれています。図鑑という名のとおり絵や図が多いので、初心者でも理解しやすくなっています。分析手法の名前から逆引きもできるので、それぞれのデータ分析手法について詳しく学びたいときにもおすすめ。辞書のように手元に置いておきたい一冊です。
※Amazon商品ページのリンクを掲載しています
おわりに
データ分析の代表的な手法を3つ紹介してきました。これらの手法を正しく活用するためには、どのような仮説を立てるかが重要です。本連載の第1回でデータ分析の一連の流れと仮説の立て方を解説しているので、そちらもぜひご覧ください。
↓ 「ゼロから始めるデータ分析」記事一覧はこちら
#1 初学者がまず知るべき「分析の8ステップ」
#2 データ分析初心者が覚えておくべき3つの分析手法
#3 データ分析初心者が知っておきたい、経営層を巻き込むコミュニケーションのポイント
#4 データ分析初心者が知っておきたい、経営層がデータ分析と分析担当者に求めるもの
#5 データ分析初心者でも経営と組織を巻き込める、現場担当者のための4つのTips
↓ ビジネスメディア『PIVOT』にて、ビジネスにデータサイエンスを活かす方法を解説しています

株式会社サイカ
ADVA Analysis部部長 西 津平
九州大学大学院工学府修了。大学院時代、原子力発電に関わる実験を通してデータ分析と統計学を学び、新卒から3年間、遊技機メーカーにて市場動向のデータ分析業務に従事。業界にとらわれずもっと広い範囲でデータ分析ができる環境を求め、2018年10月、サイカ入社。現在ADVA Analysis部の部長を務める。



