「因果推論」をテーマに、その基本概念を理解し、効果検証の実践的なアプローチについて探る本連載。第2回となる本記事では、DAG（有向非巡回グラフ） を用いて因果構造を視覚化し、仮説を整理する手法を解説します。DAGの基本概念を押さえることで、変数間の因果関係を直感的に捉え、施策の背景にある要因を明確にします。さらに、正しい因果関係の推定を妨げる可能性のある、バックドアパス（2つの変数間に見かけ上の関連性を生じさせる経路）や交絡因子（説明変数と目的変数の両方に影響を与える外部変数）の制御といった実践的なアプローチを通じ、誤った結論に陥らないための分析設計もご紹介します。

本テーマの連載内容は下記のとおりです。因果推論の活用に向けて、ぜひ他記事もご参考ください。

• 第1回「マーケティングにおける因果推論の基本と重要性」：
  マーケティングにおける因果推論の基本を解説
• 第2回 「DAG（有向非巡回グラフ）でマーケティング施策の因果構造を理解する」（本記事）：
  因果関係を正しく捉えるための基本原則を解説
• 第3回 「マーケティング実務で因果推論を活用する方法：観察データ解析による効果検証」：
  実際の効果検証にどのように因果推論の考え方を取り入れられるかを紹介

DAGとは

因果推論において変数間の関係を視覚化し、仮説の妥当性を検証するために用いられるのがDAG：Directed Acyclic Graph（有向非巡回グラフ）です。DAGは「原因と結果の地図」のようなもので、変数をノード（円や四角）で表し、因果関係を矢印（パス）で示します。マーケティング施策の効果分析においてこのツールを活用することで、複雑な因果関係を体系的に整理し、施策の効果を特定しやすくなります。特に、施策が複数の要素に影響を与える場面では、DAGは重要な役割を果たすため、因果推論に取り掛かる第一歩目として、DAGを活用して因果構造を整理することが重要です。DAGによって仮説を整理したうえで、適切な分析対象および分析手法を選択しましょう。

主な記述ルール

• ノード：変数（広告費、売り上げなど）を円で表す。
• エッジ（矢印）：直接的な因果関係を示す。A→Bの場合、Aが原因、Bが結果を表す。
• 非巡回：ループ（循環）がないことが必須。たとえば、A → B → C → A のような循環はNG。
• 条件付け：ノードを四角で囲む（詳細は後述）。

4つの基本的な因果構造

上記の記述ルールに則り、DAGを作成していきます。構造は主に以下の4種類があげられます。これらのDAGの矢印の方向は、統計的な相関ではなく因果関係を示すため、専門知識や過去の知見、文献などをもとに決める必要があります。逆に言うと、変数間の相関関係や因果関係を数値計算なしに判定できることがDAGのメリットでもあります。

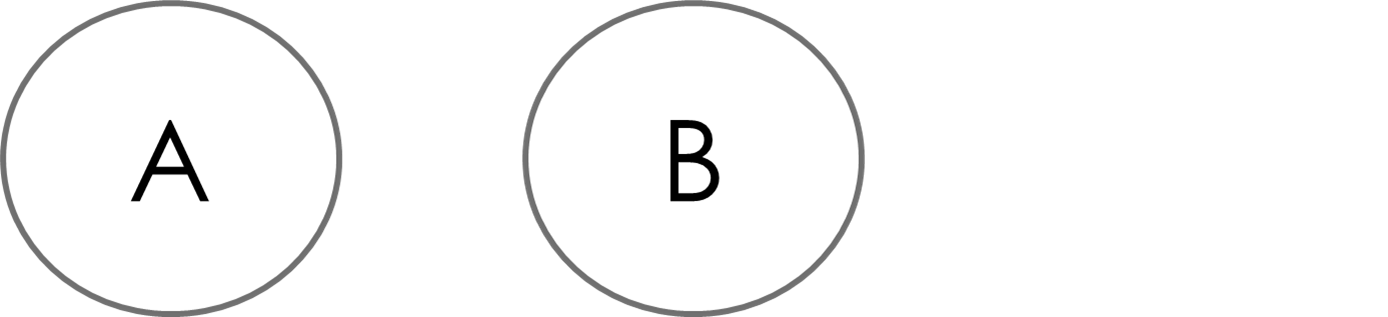
1. 完全独立

AとBの間にいかなる因果パスも存在しない構造です。

たとえば、SNS広告（A）がある商品の売上（B）に全く影響を与えない場合、この関係は「完全独立」に該当します。こうした状況の場合、売上増加の要因解明のためにはSNS広告以外の要因を検討する必要があります。

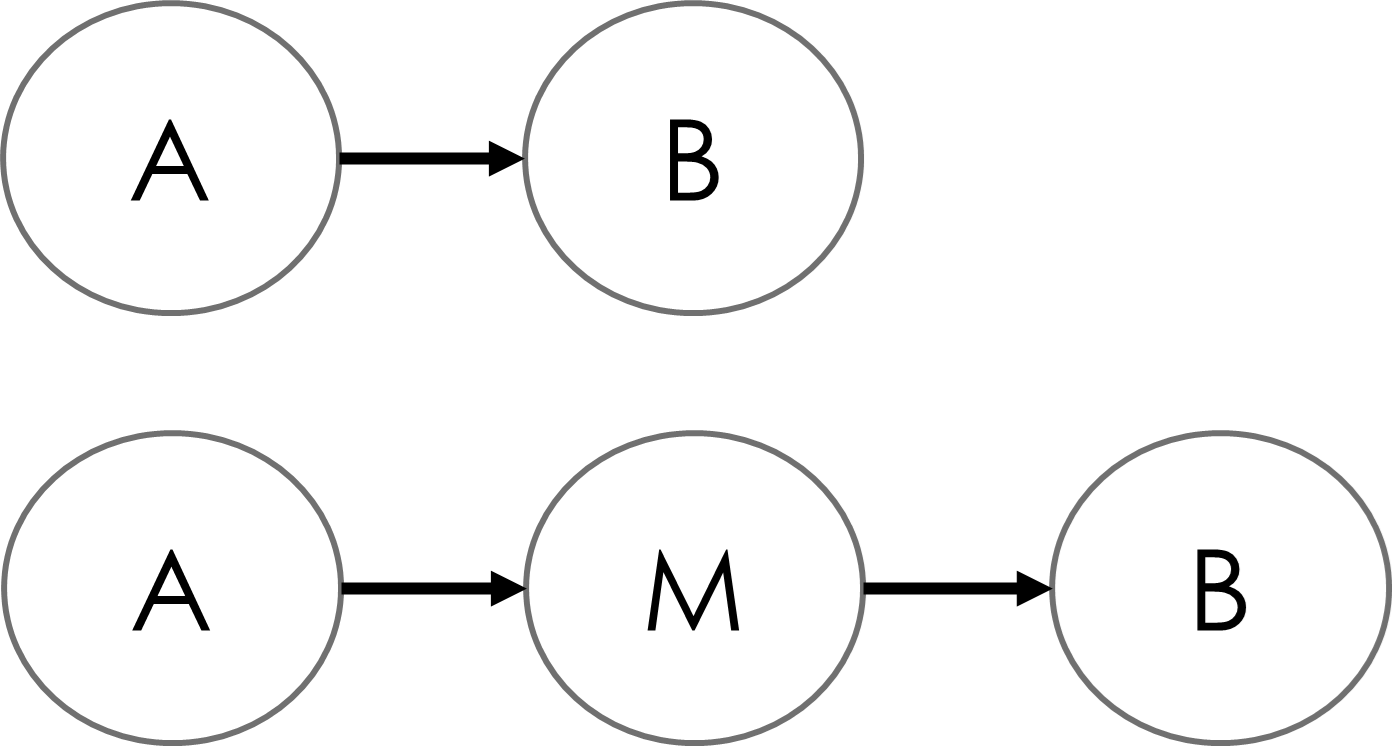
2. 連鎖

AからBに向かう矢印が一方向に続く「因果連鎖」が存在する構造です。DAGでの矢印は原因から結果に向かって伸びます。したがって、このパスは直接的かつ直列的な因果関係を表します。

たとえば、テレビCM（A）がブランド認知度（M）を高め、その結果として売上（B）が増加する場合、下記の図のように表されます。この時、M（メディエーター）は因果連鎖の中間変数として機能します。

3. フォーク（分岐）

AとBが共通の変数Cを通じて繋がる構造です。AとBの間に共通の原因が存在することを示し、このCはよく「交絡因子」と呼ばれます。

たとえば、気温（C）がアイスクリームの売上（A）と海水浴客数（B）に影響を与えている場合は、下記図のように表されます。この場合、AとBの間には見かけ上の相関関係があるため、DAGで整理しないと、アイスクリームの売上と海水浴客数の間に誤った因果関係を推測してしまう可能性があります。

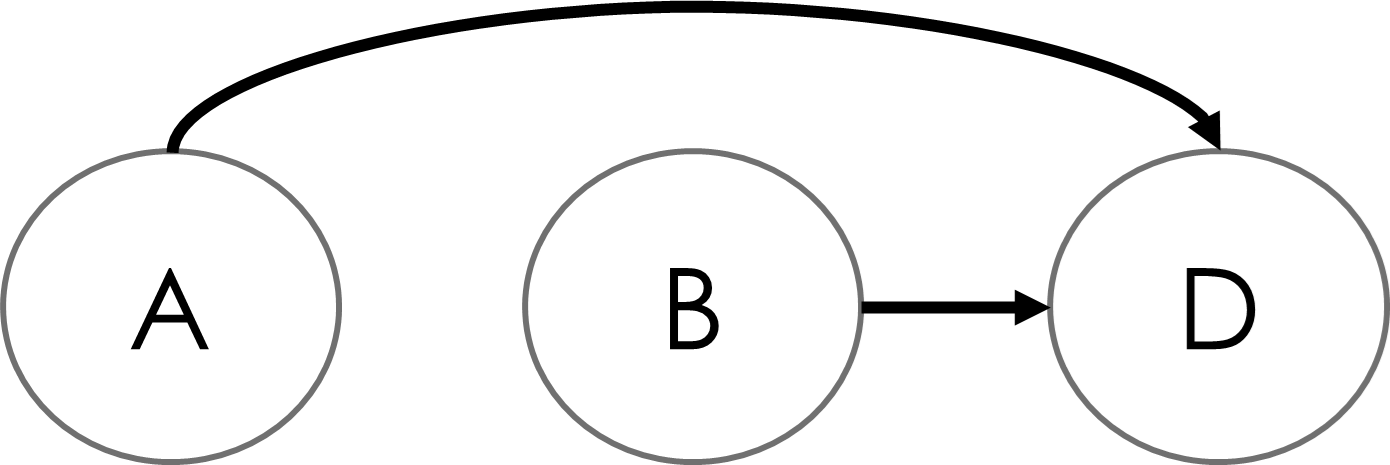
4. コライダー（合流点）

AとBが共通の結果変数Dを通じて繋がる構造です。このDは「コライダー変数」と呼ばれ、AとBに共通の結果が存在することを示します。

たとえば、新規顧客獲得数（A）と既存顧客の離脱率（B）がともに売上（D）に影響を与える場合、下記の図で表されます。

合流点となるDで条件付けすることで、AとBに偽の相関が生まれるバイアスが生まれることがあり、これを「合流点バイアス」といいます。

バックドアパスと交絡因子の制御について

因果推論においては、交絡因子を制御することが重要です（詳細は「マーケティングにおける因果推論の基本と重要性」をご覧ください）。DAGの強みは、「バックドアパス」や「合流点バイアス」といった概念を用いることで、交絡因子を制御した信頼性の高い分析設計が可能になることです。ここでは一例として、バックドアパスを用いた交絡因子の制御について説明します。

バックドアパスとは

バックドアパスは、「A から B への因果関係をゆがめる別のパス」のことです。たとえば、コートの売上（B）に対する広告費（A）の効果を推定したいとき、季節性（C）が下記の分岐構造のようにA、Bどちらにも影響を与える構造になっている場合、季節性が交絡因子として、A から B への因果関係をゆがめるパスを形成しています。

より具体的に言うと、冬はコートの売上が増える（B↑）、冬は広告費も増やす（A↑）となっている場合に、「広告費が増えたから売上が増えた」ように見えてしまいますが、実際は季節が両方に影響しているだけの可能性があります。このAからBへの直接効果以外の経路（ここではA ← C → B）をバックドアパスといいます。この例では、AからBへの直接効果とバックドアパスを経由したCによるAとBへの効果を区別することができません。この状態を、バックドアパスが開かれた状態といいます。

交絡因子の制御

それでは、交絡因子の影響を取り除くにはどうすればよいでしょうか？解決策としてバックドアを閉じるという方法があります。バックドアを閉じるとはどういうことかというと、交絡因子となっているCを「条件付け」することです。DAGとしては、下図のようにCが四角で囲われた状態が条件付けされた状態で、条件付けとは、具体的にはその変数の値を固定することです。たとえば、上記の例の場合、冬のデータのみ、もしくは冬以外のデータのみに絞って分析することです。この場合、分析期間中は「季節」という要因が一定に保たれるため、季節による影響を排除し、他の要因による影響をより明確にすることができます。

もしくは回帰分析で季節性を変数として組み込むことも条件付けになります。そうすることで、バックドアパスは閉じられ、CによるAとBへの効果を区別して、AからBへの因果効果を推定することができます。このようなアプローチにより、因果構造を視覚的に整理し交絡因子があるか、交絡因子がある場合には、どのような分析設計にすれば交絡因子の影響を取り除いたうえで因果推論ができるか、といったことが整理できます。

まとめ

覚えておくべき要点

• 変数をノード、因果関係を矢印で示すDAGを用いることで、単なる相関ではなく因果性を推定することができる
• 交絡因子やバックドアパスの概念を理解し、誤った結論を招くリスクを軽減することで、正確な施策評価が可能となる
• 因果推論の理論を基礎から応用まで理解することで、データサイエンティストとの対話や実際のマーケティングデータを使った分析設計がスムーズに進められる

このように、DAGによる因果構造の整理は、マーケティングにおける意思決定の質を大幅に向上させるための必須スキルです。次の記事「マーケティング実務で因果推論を活用する方法：観察データ解析による効果検証」では、具体的な分析手法に焦点を当て、実際の施策に応用する方法を解説します。因果推論の理論を実務に応用したい方は、引き続きぜひご一読ください。